Graphing The Greatest Integer Function

Error : Please Click on "Not a robot", then try downloading again.
(a)
Examining the number line near 12 we see that $$\lfloor 12.v\rfloor = 12$$.
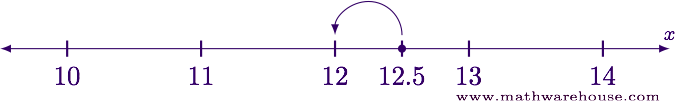
(b)
Examining the number line near -6.7 we encounter that $$\lfloor -6.7\rfloor = -vii$$.
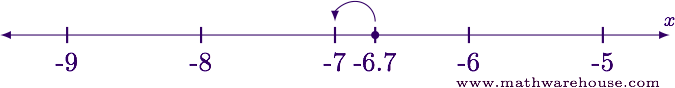
(c)
Since fifty is an integer, nosotros know $$\lfloor l\rfloor = 50$$.
(a)
Using a figurer, nosotros can determine that $$\pi$$ is approximately 3.14. Examining the number line near this indicate we run across that $$\lfloor \pi\rfloor = 3$$.

(b)
Using a calculator, we tin can determine that $$\frac{23}{19}$$ is approximately 1.21. Examining the number line near this point nosotros meet that $$\left\lfloor \frac{23}{xix}\right\rfloor = 1$$.
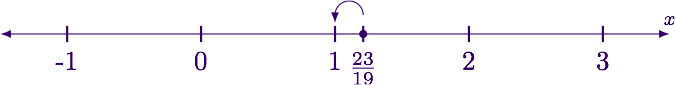
(c)
Using a reckoner, we can decide that $$\sqrt ii$$ is approximately 1.41. Examining the number line nigh this signal nosotros meet that $$\left\lfloor \sqrt 2\right\rfloor = i$$.

Step ane
Every bit in the previous example, we tin go almost this by constructing a table, or interpreting the part in terms of transformations. This solution will practice both.
TABLE
$$ \begin{array}{|c|c|c|} \hline ten & 2x & \lfloor 2x \rfloor \\ \hline -0.75 & -1.5 & -2\\ -0.five & -one & -1\\ -0.25 & -0.5 & -1\\ 0 & 0 & 0\\ 0.25 & 0.5 & 0\\ 0.five & ane & 1\\ 0.75 & i.5 & 1\\ 1 & 2 & 2\\ 1.25 & two.5 & two\\ \hline \end{array} $$
In this case, we encounter that every time $$ten$$ is a multiple of 0.five the function jumps to the next higher integer.
TRANSFORMATION
We can interpret $$y = \lfloor 2x \rfloor$$ as a horizontal pinch by a factor of ii. That is, each of the $$x$$-values from $$y = \lfloor x\rfloor$$ gets cut in one-half, just the $$y$$-values stay the same.
Answer
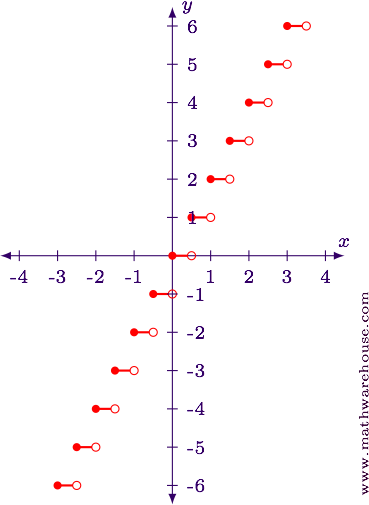
Footstep 1
We will examine this part using both a table, and and so as a transformation of functions.
TABLE
$$ \brainstorm{array}{|c|c|c|} \hline x & 1.5x & \lfloor 1.5x \rfloor \\ \hline -one & -1.5 & -2\\ -two/3 & -ane & -1\\ -1/3 & -0.five & -one\\ 0 & 0 & 0\\ 1/3 & 0.5 & 0\\ ii/three & 1 & 1\\ 1 & 1.5 & 1\\ 4/iii & two & ii\\ 5/3 & 2.5 & 2\\ 2 & three & 3\\ \hline \end{array} $$
The table shows that the function increases every multiple of 2/3.
TRANSFORMATION
Since the variable $$x$$ is being multiplied by 1.5, we know that the graph of $$y = \lfloor x\rfloor$$ is existence compressed horizontally.
Answer
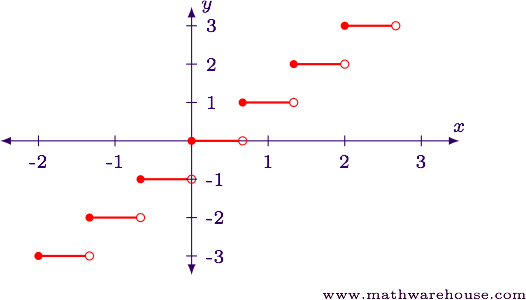
Pace one
Nosotros volition examine this function using both a table, and then as a transformation of functions.
Table
$$ \begin{assortment}{|c|c|c|} \hline 10 & -0.25x & \lfloor -0.25x \rfloor \\ \hline -iv & 1 & 1\\ -3 & 0.75 & 0\\ -2 & 0.5 & 0\\ -ane & 0.25 & 0\\ 0 & 0 & 0\\ i & -0.25 & -1\\ 2 & -0.5 & -1\\ 3 & -0.75 & -1\\ four & -one & -i\\ \hline \end{array} $$
The table shows that the part increases every multiple of 4.
TRANSFORMATION
Since the variable $$10$$ is being multiplied past 0.25, we know the function is existence horizontally stretched by a gene of 4. Since the coefficient is negative, the part is as well being reflected about the $$y$$-axis.
Answer
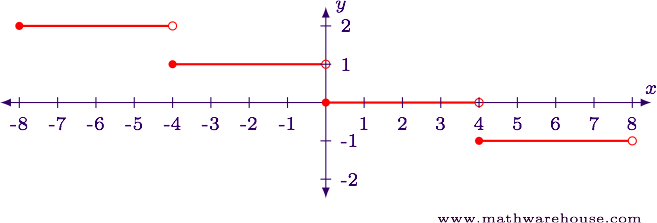
Step 1
We will examine this function using both a table, and and so as a transformation of functions.
Table
$$ \begin{assortment}{|c|c|c|} \hline x & \lfloor x \rfloor & 2\lfloor x \rfloor\\ \hline -ane.five & -2 & -iv\\ -one & -1 & -2\\ -0.5 & -1 & -2\\ 0 & 0 & 0\\ 0.5 & 0 & 0\\ 1 & 1 & two\\ 1.5 & 1 & 2\\ 2 & 2 & 4\\ \hline \end{array} $$
The table shows that the function increases by ii every time $$x$$ increases by 1.
TRANSFORMATIONS
The office has a vertical stretch past ii.
Answer
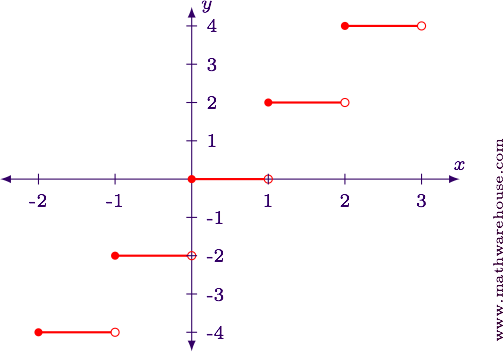
Stride 1
Nosotros will examine this role using both a tabular array, and then as a transformation of functions.
Tabular array
$$ \begin{array}{|c|c|c|} \hline x & ten + 3 & \lfloor x + iii\rfloor \\ \hline -4 & -1 & -1\\ -3.v & -0.5 & -1\\ -iii & 0 & 0\\ -2.5 & -0.5 & 0\\ -two & i & 1\\ -1.5 & ane.5 & 1\\ -1 & ii & two\\ -0.5 & ii.5 & 2\\ 0 & three & three\\ 0.five & 3.five & 3\\ 1 & 4 & 4\\ \hline \finish{array} $$
The table shows us that the office increases each time $$x$$ is an integer.
TRANSFORMATIONS
The function $$y = \lfloor x + iii\rfloor$$ is a shift to the left by iii units of the office
Answer
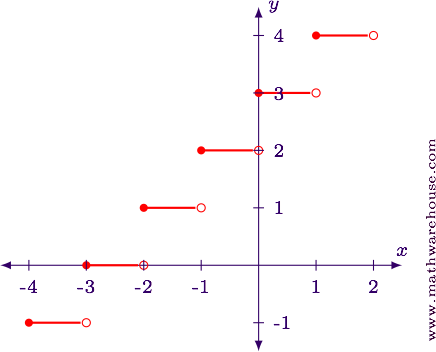
Footstep 1
We will examine this function using both a tabular array, and and so as a transformation of functions.
TABLE
$$ \begin{assortment}{|c|c|c|c|} \hline 10 & 2 - x & \lfloor two - x \rfloor & -0.75\lfloor ii - 10 \rfloor\\ \hline -ii.5 & 4.5 & 4 & 3\\ -2 & 4 & iv & three\\ -1.5 & three.v & three & two.25\\ -ane & 3 & 3 & 2.25\\ -0.five & ii.v & 2 & one.5\\ 0 & 2 & 2 & 1.5\\ 0.5 & 1.5 & 1 & 0.75\\ ane & 1 & ane & 0.75\\ ane.v & 0.v & 0 & 0\\ ii & 0 & 0 & 0\\ ii.5 & -0.5 & -1 & -0.75\\ \hline \terminate{assortment} $$
The table shows that the function changes value just after $$ten$$ is an integer. Each time the function changes value it decreases past 0.75.
TRANSFORMATIONS
The function $$y = -0.75\lfloor 2 - 10\rfloor$$ consists of four different transformations.
- A vertical reflection (over the $$ten$$-axis).
- A horizontal reflection (over the $$y$$-axis).
- A vertical compression of 0.75.
- A horizontal shift by 2 units to the correct.
Answer
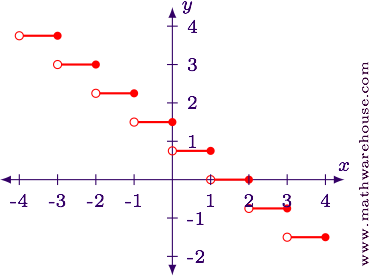
Footstep 1
Since the reciprocal function $$y = \frac 1 x$$ is not a standard transformation, we will merely apply a table to understand the behavior of this function.
Table
$$ \begin{array}{|c|c|c|} \hline x & i/ten & \left\lfloor 1/x \right\rfloor \\ \hline -4 & -ane/4 & -one\\ -3 & -1/3 & -one\\ -2 & -1/ii & -i\\ -one & -i & -1\\ -1/2 & -ii & -2\\ -i/3 & -3 & -3\\ -1/iv & -4 & -4\\ 0 & \mbox{undefined} & -\\ 1/4 & iv & 4\\ 1/three & 3 & 3\\ 1/2 & 2 & two\\ one & 1 & 1\\ 2 & 1/2 & 0\\ 3 & 1/3 & 0\\ 4 & 1/4 & 0\\ \hline \end{array} $$
Respond
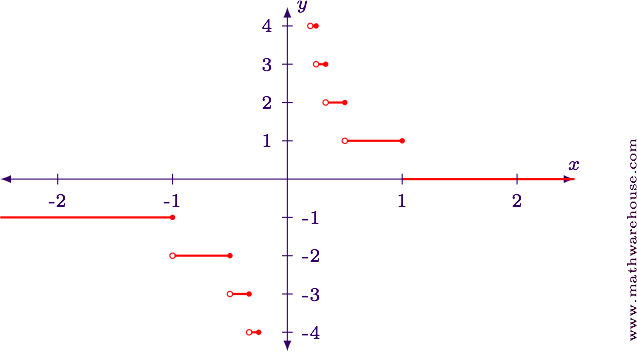
Pace 1
Since the reciprocal function $$y = \frac i x$$ is not a standard transformation, we will simply use a table to empathize the behavior of this function.
TABLE
$$ \brainstorm{array}{|c|c|c|} \hline ten & \lfloor 10\rfloor & \frac 1 {\lfloor 10 \rfloor} \\ \hline -4 & -4 & -1/4\\ -3 & -iii & -ane/3\\ -ii & -two & -one/2\\ -1 & -1 & -1\\ 0 & 0 & \mbox{undefined}\\ i & 1 & i\\ 2 & 2 & i/2\\ iii & three & one/3\\ 4 & 4 & one/4\\ \hline \end{assortment} $$
Reply
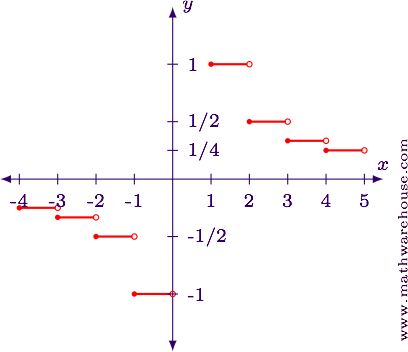
Stride one
We'll examine the behavior of this function by amalgam a table of values.
TABLE
$$ \begin{array}{|c|c|c|} \hline ten & x^2 & \lfloor x^ii\rfloor \\ \hline -ii & 4 & 4\\ -\sqrt iii & iii & 3\\ -\sqrt two & 2 & 2\\ -one & 1 & 1\\ -0.5 & 0.25 & 0\\ 0 & 0 & 0\\ 0.5 & 0.25 & 0\\ 1 & 1 & i\\ \sqrt two & ii & two\\ \sqrt 3 & iii & 3\\ 2 & 4 & 4\\ \hline \end{array} $$
Answer
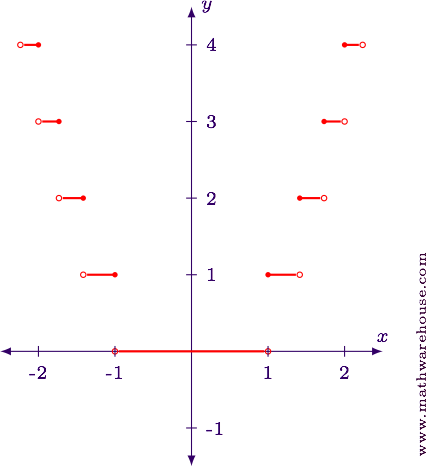
Footstep ane
We'll examine the beliefs of this function by constructing a tabular array of values.
TABLE
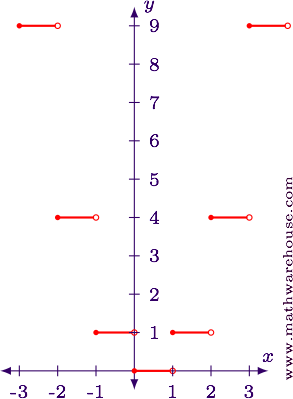
$$ \brainstorm{assortment}{|c|c|c|} \hline ten & \lfloor ten\rfloor & \lfloor x\rfloor^2\\ \hline -three & -three & 9\\ -2.5 & -3 & 9\\ -2 & -2 & 4\\ -one.v & -2 & four\\ -ane & -1 & 1\\ -0.5 & -1 & 1\\ 0 & 0 & 0\\ 0.5 & 0 & 0\\ 1 & 1 & 1\\ 1.5 & 1 & 1\\ two & 2 & 4\\ 2.5 & two & four\\ 3 & three & 9\\ \hline \finish{assortment} $$
Answer
Footstep 1
Permit's build a tabular array of values to empathise this function.
Tabular array
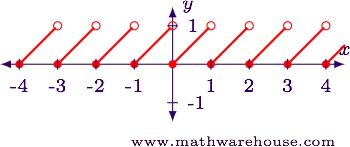
$$ \begin{array}{|c|c|c|} \hline x & x \lfloor ten\rfloor & x - \lfloor x\rfloor\\ \hline -one & -ane & 0\\ -0.8 & -1 & 0.2\\ -0.6 & -1 & 0.4\\ -0.iv & -i & 0.half-dozen\\ -0.2 & -1 & 0.8\\ 0 & 0 & 0\\ 0.2 & 0 & 0.two\\ 0.4 & 0 & 0.iv\\ 0.6 & 0 & 0.6\\ 0.viii & 0 & 0.eight\\ 1 & ane & 0\\ 1.2 & 1 & 0.ii\\ 1.4 & 1 & 0.iv\\ \hline \end{array} $$
Each time $$x$$ is an integer, the office resets to 0. Then it slowly increases towards 1.
Reply
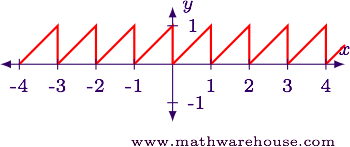
NOTE: This office is an example of a sawtooth wave. It is called this considering, if we connect the points that are vertically aligned (run across below) the graph resembles the teeth of a saw. Sawtooth waves play an of import role in music and in representations of various moving ridge forms in electronics and applied science.
Stride one
Make a modify of variable so the equation is easier to work with. Specifically, permit $$u = \lfloor ane.3x\rfloor$$.
$$ \begin{align*} \lfloor 5.4 - \blueish{\lfloor 1.3x \rfloor}\rfloor & = 17\\ \lfloor 5.iv - \blue{u}\rfloor & = 17\\ \end{align*} $$
Step ii
Supplant the equation with ane of the inequalities discussed in a higher place. Then solve for $$u$$.
$$ \begin{align*}% 17 & \leq 5.4 - u < 18\\ 17 - five.4 & \leq - u < xviii-5.four\\ 11.6 & \leq - u < 12.6\\ -11.6 & \geq u > -12.6 \end{marshal*} $$
Since $$u$$ must be an integer, we know that $$u = -12$$.
Stride iii
Replace $$u$$ in the equation.
$$ \begin{align*}% \blue u & = -12\\ \blue{\lfloor i.3x\rfloor} & = -12 \finish{align*} $$
Step iv
Replace the equation with ane of the inequalities, then solve.
$$ \begin{marshal*} -12 & \leq 1.3x < -11\\[6pt] -\frac{12}{1.iii} & \leq x < -\frac{xi}{one.3}\\[6pt] -\frac{120}{13} & \leq 10 < -\frac{110}{13}\\[6pt] -9.2307 & \leq x < -eight.4615 \stop{align*} $$
Answer
In interval note, $$x \in \left[-\frac{120}{13}, -\frac{110}{13}\right)$$.
Step i
Brand a change of variable so the equation is easier to piece of work with. Specifically, permit $$\bluish{u = \lfloor ii.5x-7.ix\rfloor}$$.
$$ \brainstorm{marshal*} \lfloor three.two + \bluish{\lfloor two.5x - vii.9\rfloor}\rfloor & = -5\\ \lfloor 3.2 + \blueish{u}\rfloor & = -5 \cease{marshal*} $$
Step 2
Replace the equation with one of the inequalities, and solve for $$u$$.
$$ \begin{marshal*} -five & \leq 3.two + u < -4\\ -5 - three.2 & \leq u < -four - three.2\\ -viii.two & \leq u < -7.2 \end{align*} $$
Since $$u$$ has to be an integer, we know $$u = -8$$.
Step 3
Substitute the value of $$u$$ dorsum into the equation.
$$ \begin{align*} \blue{u} & = -8\\ \blueish{\lfloor 2.5x-7.9\rfloor} & = -8\\ \end{marshal*} $$
Stride iv
Supplant the equation with one of the inequalities and solve for $$ten$$.
$$ \begin{align*} -eight & \leq two.5x-seven.9 < -7\\ -8 + 7.ix & \leq ii.5x < -7 + seven.9\\ -0.ane & \leq 2.5x < 0.9\\ -\frac{0.ane}{ii.5} & \leq x < \frac{0.nine}{2.5}\\[6pt] -\frac 1 {25} & \leq 10 < \frac 9 {25}\\[6pt] -0.04 & \leq 10 < 0.36 \end{align*} $$
Answer
In interval note, $$x \in [-0.04, 0.36]$$.
Return to lesson

Error : Delight Click on "Not a robot", then endeavour downloading again.
Graphing The Greatest Integer Function,
Source: https://www.mathwarehouse.com/algebra/greatest-integer-function-and-graph-practice-problems.php
Posted by: nolanheigher.blogspot.com


0 Response to "Graphing The Greatest Integer Function"
Post a Comment